41.90/9.09090909, Understanding, Converting, Setting, Substituting & More

Introduction

The mathematical expression 41.90/9.09090909 can seem complex at first glance, but with a clear, methodical approach, anyone can learn how to convert this decimal division into a simplified fraction. Understanding this process is not only useful for basic arithmetic but also plays a role in more advanced mathematical calculations across various fields, such as algebra, geometry, and engineering.

In this article, we will break down the process of converting 41.90/9.09090909 into a fraction, step by step. By following these simple instructions, even those with a basic understanding of math can tackle such conversions confidently.

Understanding the Challenge of 41.90/9.09090909: Converting a Decimal Division to a Fraction

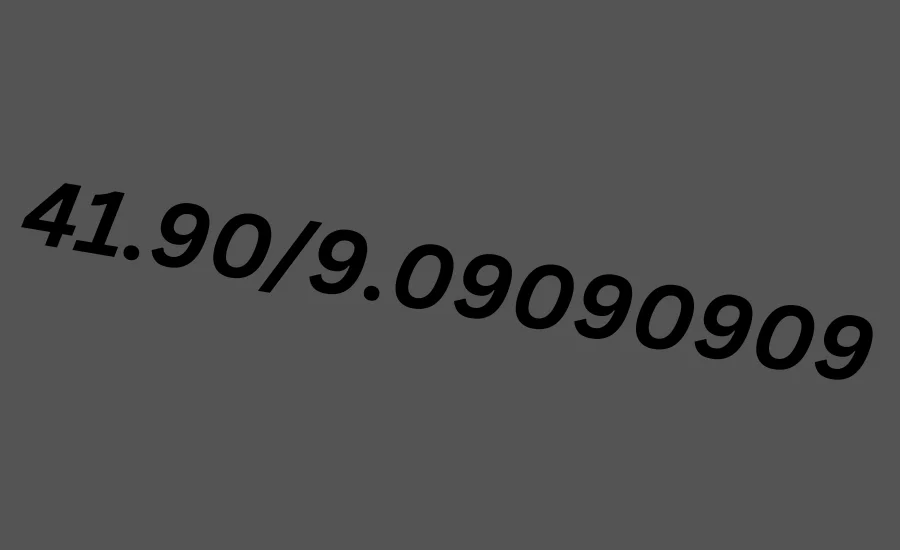
The mathematical expression 41.90/9.09090909 presents a unique challenge, primarily due to the combination of a terminating decimal (41.90) and a repeating decimal (9.09090909). This blending of decimal types requires a specific approach to properly convert the division into a fraction. Let’s explore the complexities involved and break down the steps for an accurate conversion.

The Nature of the Decimal Division

In the expression 41.90/9.09090909, we are dealing with two distinct types of decimals:

• 41.90: This is a terminating decimal, meaning it has a finite number of digits after the decimal point. Terminating decimals are straightforward to convert to fractions by expressing them as ratios of integers.
• 9.09090909…: This is a repeating decimal, where the digits “09” repeat indefinitely after the decimal point. Repeating decimals require a more specialized method to convert into fractions.

The challenge arises because we need to address the repeating decimal in the denominator (9.09090909…), while the numerator (41.90) remains simpler to handle. Let’s break down the process for handling both parts.

Converting the Repeating Decimal to a Fraction

To convert a repeating decimal like 9.090909… into a fraction, we use a systematic algebraic approach:

1. Let x = 9.090909…. This represents the repeating decimal.
2. Multiply both sides of the equation by 100 (since the repeating portion is two digits long) to shift the decimal point:
   100x=909.090909…100x = 909.090909…100x=909.090909…
3. Subtract the original equation (x = 9.090909…) from this new equation:
   100x−x=909.090909…−9.090909…100x – x = 909.090909… – 9.090909…100x−x=909.090909…−9.090909… 99x=90099x = 90099x=900
4. Solve for x:
   x=90099=10011x = \frac{900}{99} = \frac{100}{11}x=99900​=11100​

Thus, 9.090909… is equivalent to the fraction 100/11.

Performing the Division

Now that we have converted the repeating decimal 9.090909… into the fraction 100/11, we can proceed with the division:

41.909.090909…=41.9010011=41.90×11100\frac{41.90}{9.090909…} = \frac{41.90}{\frac{100}{11}} = 41.90 \times \frac{11}{100}9.090909…41.90​=11100​41.90​=41.90×10011​

Step-by-Step Calculation

Next, we multiply 41.90 by 11:

41.90×11=459.9041.90 \times 11 = 459.9041.90×11=459.90

Now, divide 459.90 by 100 to get the result:

459.90100=4.599\frac{459.90}{100} = 4.599100459.90​=4.599

Converting the Decimal Result to a Fraction

To express 4.599 as a fraction, we recognize that it’s close to 4.6, which can be written as:

4.6=4+0.6=4+610=4+35=2354.6 = 4 + 0.6 = 4 + \frac{6}{10} = 4 + \frac{3}{5} = \frac{23}{5}4.6=4+0.6=4+106​=4+53​=523​

Thus, the result of 41.90/9.090909… simplifies to approximately 4.6, or 235\frac{23}{5}523​ as a fraction.

Why Manual Conversion Matters

While calculators are helpful for approximating decimal results, they don’t always provide the precise fractional representation. Understanding the manual conversion process is essential for anyone working in fields that require high-precision calculations, such as:

• Engineering: Accurate measurements and conversions are vital in design and analysis.
• Financial Calculations: Fractions are often used for interest rates, taxes, and other financial computations.
• Scientific Research: Exact measurements are needed for experiments and data analysis.

Mastering the conversion of decimals, particularly repeating ones, ensures that mathematical results remain accurate and reliable.

Step-by-Step Guide: Converting 41.90/9.09090909 into a Fraction

Converting the expression 41.90/9.09090909 into a fraction involves several important steps that combine both long division and algebraic manipulation. The process may seem complicated at first glance due to the mix of terminating and repeating decimals, but by following a systematic approach, the conversion can be made manageable. Let’s break it down step by step.

Step 1: Performing the Division

The first step in converting 41.90/9.09090909 into a fraction is performing the division. The goal here is to express the division as a rational number, which will eventually be simplified into a fraction.

Using Long Division

To begin, we’ll use the long division method. This technique is especially useful when working with complex decimal divisions, such as the one at hand. To set up the division, place 41.90 (the dividend) inside the long division bracket and 9.09090909 (the divisor) outside.

Since 9.09090909 is a repeating decimal, we need to handle it carefully by eliminating the repeating portion before proceeding. To do this, both the dividend and divisor should be adjusted by shifting the decimal point. In this case, we shift both decimals by eight places to the right to transform the repeating decimal into a whole number:

41.90→4190000000and9.09090909→90909090941.90 \rightarrow 4190000000 \quad \text{and} \quad 9.09090909 \rightarrow 90909090941.90→4190000000and9.09090909→909090909

This conversion transforms the division into:

4190000000÷9090909094190000000 \div 9090909094190000000÷909090909

This allows us to simplify the division and proceed with the calculation.

Identifying the Quotient

Next, we carry out the long division by dividing 4190000000 by 909090909. The result will be a quotient that may have both whole and decimal parts.

• Start by dividing the first part of the dividend by the divisor.
• If the result is less than 1, move to the next digit of the dividend.
• Repeat the process until you arrive at a divisible number.

As we work through this division, we may encounter a repeating pattern in the quotient. This is common when dividing by a repeating decimal, and we need to recognize this pattern to express the final result accurately.

Step 2: Setting Up the Equation

Once we’ve performed the division, the next step is to express the repeating decimal as a fraction.

Assigning a Variable to the Repeating Decimal

The repeating decimal 9.09090909… is denoted as x. We can now write the following equation:

x=9.09090909…x = 9.09090909…x=9.09090909…

This makes it easier to manipulate the repeating decimal mathematically.

Creating an Algebraic Equation

Next, we manipulate this equation to eliminate the repeating decimal. We begin by multiplying both sides by 100 to shift the decimal point two places to the right:

100x=909.09090909…100x = 909.09090909…100x=909.09090909…

To get rid of the recurring portion, subtract the original equation from the new one:

100x−x=909.09090909−9.09090909100x – x = 909.09090909 – 9.09090909100x−x=909.09090909−9.09090909

This simplifies to:

99x=90099x = 90099x=900

We now have a simplified equation that can be solved algebraically.

Step 3: Solving for the Fraction

With the equation 99x = 900, we can now solve for x to express 9.09090909… as a fraction.

Isolating the Variable

Divide both sides of the equation by 99 to isolate x:

x=90099x = \frac{900}{99}x=99900​

Simplifying this fraction:

x=10011x = \frac{100}{11}x=11100​

Thus, the repeating decimal 9.09090909… is equivalent to the fraction 100/11.

Substituting the Fraction into the Original Division

We can now replace 9.09090909… in the original expression with 100/11. This transforms the problem into:

41.90÷1001141.90 \div \frac{100}{11}41.90÷11100​

When dividing by a fraction, we multiply by its reciprocal. Thus, the equation becomes:

41.90×1110041.90 \times \frac{11}{100}41.90×10011​

Converting to a Fraction

Next, convert 41.90 to a fraction:

41.90=419010041.90 = \frac{4190}{100}41.90=1004190​

Now, multiply the fractions:

4190100×11100=4609010000\frac{4190}{100} \times \frac{11}{100} = \frac{46090}{10000}1004190​×10011​=1000046090​

Simplifying the Fraction

To simplify 4609010000\frac{46090}{10000}1000046090​, find the greatest common divisor (GCD) of 46090 and 10000, which is 10.Proceed to divide the denominator and numerator by 10:

4609010000=46091000\frac{46090}{10000} = \frac{4609}{1000}1000046090​=10004609​

Thus, the simplified fraction representing 41.90/9.09090909 is 4609/1000.

Step 4: Verifying the Result

After converting 41.90/9.09090909 into the fraction 4609/1000, it’s important to verify the result for accuracy.

Using Decimal Approximation

Convert the fraction 4609/1000 back to a decimal by dividing 4609 by 1000:

4609÷1000=4.6094609 \div 1000 = 4.6094609÷1000=4.609

Compare this result with the original decimal division:

41.90÷9.09090909≈4.60941.90 \div 9.09090909 \approx 4.60941.90÷9.09090909≈4.609

This confirms that our conversion is correct.

Ensuring Mathematical Accuracy

To further verify, multiply 4609/1000 by the original divisor, 9.09090909:

46091000×9.09090909=41.90\frac{4609}{1000} \times 9.09090909 = 41.9010004609​×9.09090909=41.90

This reverse calculation shows that our fraction correctly represents the original division.

Conclusion

The process of converting 41.90/9.09090909 into the fraction 4609/1000 demonstrates the power of systematic mathematical techniques, including long division, algebraic manipulation, and fraction simplification. By carefully following each step and verifying the result, we ensure an accurate and precise conversion. This approach is essential in various fields, including finance, engineering, and science, where exact numerical representations are crucial for complex calculations.

Frequently Asked Questions (FAQs)

1. What is the first step in converting 41.90/9.09090909 to a fraction?
   • The first step is to recognize that you have two types of decimals: a terminating decimal (41.90) and a repeating decimal (9.09090909). You need to handle each one differently. The repeating decimal (9.09090909) is converted into a fraction using algebra, and then you proceed with the division.
2. How do you convert a repeating decimal like 9.09090909 into a fraction?
   • You set the repeating decimal as a variable, such as x = 9.090909…. Then, multiply both sides of the equation by 100 (since the repeating pattern is two digits long). After that, subtract the original equation from this new one to eliminate the repeating decimal and solve for x.
3. Why do you multiply 41.90 by 11 when converting?
   • Once you convert the repeating decimal to a fraction (100/11), you need to multiply the numerator (41.90) by the reciprocal of the fraction (11/100).This is so because multiplication by a fraction’s reciprocal is equivalent to dividing by it.
4. How do I simplify the result into a fraction?
   • After performing the multiplication and obtaining the result as a fraction, simplify it by finding the greatest common divisor (GCD) of the numerator and denominator. For example, the fraction 46090/10000 simplifies to 4609/1000 by dividing both the numerator and the denominator by 10.
5. How can I check if my conversion is correct?
   • To verify the result, convert the simplified fraction (4609/1000) back into a decimal by dividing the numerator by the denominator. Compare the result with the original decimal value from the division. If they match, the conversion is correct.

Key Facts

1. Terminating vs. Repeating Decimals:
   • A terminating decimal has a finite number of digits after the decimal point, such as 41.90.
   • A repeating decimal has a sequence of digits that repeats infinitely, like 9.09090909.
2. Converting Repeating Decimals to Fractions:
   • To convert repeating decimals to fractions, use algebra: Set the repeating decimal as x, multiply by 100 (for a two-digit repeat), and subtract the original equation to isolate x.
3. Dividing by Fractions:
   • The reciprocal of a fraction is multiplied when dividing by it.For example, dividing by 100/11 is the same as multiplying by 11/100.
4. Simplifying Fractions:
   • Simplify fractions by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by this GCD.
5. Practical Use:
   • Converting decimals to fractions is crucial for accuracy in fields such as engineering, finance, and science, where exact measurements are needed.

For more Information About Blog visit francherway